39 lines
1.1 KiB
Markdown
39 lines
1.1 KiB
Markdown
|
|
---
|
||
|
|
source:
|
||
|
|
platform: leetcode
|
||
|
|
problemId: 1584
|
||
|
|
tags: graphs, prims-algorithm
|
||
|
|
---
|
||
|
|
|
||
|
|
You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
|
||
|
|
|
||
|
|
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
|
||
|
|
|
||
|
|
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
|
||
|
|
|
||
|
|
**Example 1:**
|
||
|
|
|
||
|
|
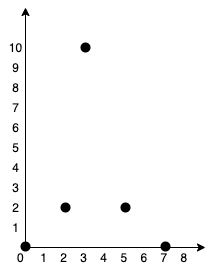
|
||
|
|
|
||
|
|
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
|
||
|
|
Output: 20
|
||
|
|
Explanation:
|
||
|
|
|
||
|
|
We can connect the points as shown above to get the minimum cost of 20.
|
||
|
|
Notice that there is a unique path between every pair of points.
|
||
|
|
|
||
|
|
|
||
|
|
**Example 2:**
|
||
|
|
|
||
|
|
Input: points = [[3,12],[-2,5],[-4,1]]
|
||
|
|
Output: 18
|
||
|
|
|
||
|
|
|
||
|
|
**Constraints:**
|
||
|
|
|
||
|
|
* `1 <= points.length <= 1000`
|
||
|
|
* `-106 <= xi, yi <= 106`
|
||
|
|
* All pairs `(xi, yi)` are distinct.
|
||
|
|
|
||
|
|
https://leetcode.com/problems/min-cost-to-connect-all-points/
|