num of connected components in undirected graph
This commit is contained in:
parent
f079950230
commit
910bc98e85
@ -0,0 +1,22 @@
|
||||
You have a graph of `n` nodes. You are given an integer `n` and an array `edges` where `edges[i] = [ai, bi]` indicates that there is an edge between `ai` and `bi` in the graph.
|
||||
|
||||
Return _the number of connected components in the graph_.
|
||||
|
||||
Example 1: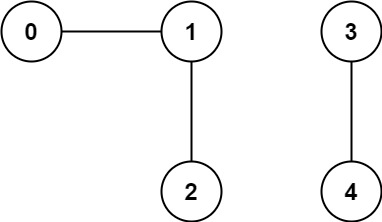
|
||||
|
||||
Input: n = 5, edges = [[0,1],[1,2],[3,4]] Output: 2
|
||||
|
||||
Example 2: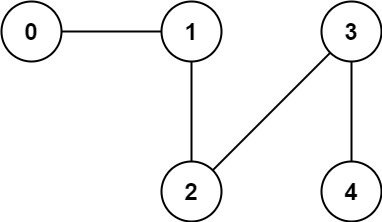
|
||||
|
||||
Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]] Output: 1
|
||||
|
||||
Constraints:
|
||||
|
||||
* `1 <= n <= 2000`
|
||||
* `1 <= edges.length <= 5000`
|
||||
* `edges[i].length == 2`
|
||||
* `0 <= ai <= bi < n`
|
||||
* `ai != bi`
|
||||
* There are no repeated edges.
|
||||
|
||||
https://leetcode.com/problems/number-of-connected-components-in-an-undirected-graph/
|
||||
@ -0,0 +1,45 @@
|
||||
# Time: O(E · 𝛼(n)) ; 𝛼(n) is inverse Ackermann function
|
||||
# Space: O(V)
|
||||
|
||||
|
||||
class Solution:
|
||||
def countComponents(self, n: int, edges: List[List[int]]) -> int:
|
||||
parent = [i for i in range(n)]
|
||||
|
||||
# Or like sizes of the components
|
||||
rank = [1] * n
|
||||
|
||||
def find(node):
|
||||
# Parent of node could be itself (i.e, no parent)
|
||||
current_node = node
|
||||
|
||||
while current_node != parent[current_node]:
|
||||
# Path compression to speed up union-find
|
||||
parent[current_node] = parent[parent[current_node]]
|
||||
current_node = parent[current_node]
|
||||
|
||||
return current_node
|
||||
|
||||
|
||||
def union(a, b):
|
||||
parent_a, parent_b = find(a), find(b)
|
||||
|
||||
if parent_a == parent_b:
|
||||
return 0
|
||||
|
||||
if rank[parent_a] > rank[parent_b]:
|
||||
parent[parent_a] = parent_b
|
||||
rank[parent_b] += rank[parent_a]
|
||||
else:
|
||||
parent[parent_b] = parent_a
|
||||
rank[parent_a] += rank[parent_b]
|
||||
|
||||
return 1
|
||||
|
||||
|
||||
result = n
|
||||
for a, b in edges:
|
||||
result -= union(a, b)
|
||||
|
||||
return result
|
||||
|
||||
Loading…
Reference in New Issue
Block a user