min-cost-to-connect-all-points py3
This commit is contained in:
parent
9bf1a027c0
commit
950abb6b37
38
1706_min-cost-to-connect-all-points/README.md
Normal file
38
1706_min-cost-to-connect-all-points/README.md
Normal file
@ -0,0 +1,38 @@
|
||||
---
|
||||
source:
|
||||
platform: leetcode
|
||||
problemId: 1584
|
||||
tags: graphs, prims-algorithm
|
||||
---
|
||||
|
||||
You are given an array `points` representing integer coordinates of some points on a 2D-plane, where `points[i] = [xi, yi]`.
|
||||
|
||||
The cost of connecting two points `[xi, yi]` and `[xj, yj]` is the **manhattan distance** between them: `|xi - xj| + |yi - yj|`, where `|val|` denotes the absolute value of `val`.
|
||||
|
||||
Return _the minimum cost to make all points connected._ All points are connected if there is **exactly one** simple path between any two points.
|
||||
|
||||
**Example 1:**
|
||||
|
||||
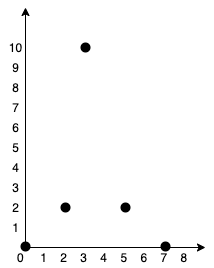
|
||||
|
||||
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
|
||||
Output: 20
|
||||
Explanation:
|
||||
|
||||
We can connect the points as shown above to get the minimum cost of 20.
|
||||
Notice that there is a unique path between every pair of points.
|
||||
|
||||
|
||||
**Example 2:**
|
||||
|
||||
Input: points = [[3,12],[-2,5],[-4,1]]
|
||||
Output: 18
|
||||
|
||||
|
||||
**Constraints:**
|
||||
|
||||
* `1 <= points.length <= 1000`
|
||||
* `-106 <= xi, yi <= 106`
|
||||
* All pairs `(xi, yi)` are distinct.
|
||||
|
||||
https://leetcode.com/problems/min-cost-to-connect-all-points/
|
||||
69
1706_min-cost-to-connect-all-points/python3/solution.py
Normal file
69
1706_min-cost-to-connect-all-points/python3/solution.py
Normal file
@ -0,0 +1,69 @@
|
||||
# Time: O(N^2·logN)
|
||||
# Space: O(N^2) ; we could be pushing N·N(N - 1) / 2 edges into the heap
|
||||
from collections import defaultdict
|
||||
from heapq import heappush, heappop
|
||||
|
||||
class Solution:
|
||||
def minCostConnectPoints(self, points: List[List[int]]) -> int:
|
||||
'''
|
||||
BFS + Prim's algorithm
|
||||
'''
|
||||
N = len(points)
|
||||
neighbors = defaultdict(list)
|
||||
|
||||
# Build adjacency lists by connecting each point to every other
|
||||
# point since we are building a new graph here
|
||||
for i in range(N):
|
||||
x1, y1 = points[i]
|
||||
|
||||
for j in range(i + 1, N):
|
||||
x2, y2 = points[j]
|
||||
|
||||
# We are considering the Manhattan Distance as stated in
|
||||
# the problem
|
||||
distance = abs(x1 - x2) + abs(y1 - y2)
|
||||
|
||||
# We are going to add both the neighbor of given point as
|
||||
# well as the distance so that we can later use it to create
|
||||
# Prim's min heap
|
||||
neighbors[i].append((distance, j))
|
||||
neighbors[j].append((distance, i))
|
||||
|
||||
|
||||
# Perform Prim's algorithm
|
||||
|
||||
# To avoid cycles
|
||||
visited = set()
|
||||
|
||||
# We start at the first point, distance would be 0 since it's the first
|
||||
# point
|
||||
min_heap = [(0, 0)]
|
||||
|
||||
# We need to find distances from one node to all other nodes (as long as
|
||||
# its not already visited), keep track of it in the min heap and once
|
||||
# all neighbors of a node is visited, we should have found the next node
|
||||
# to pop from the heap since it'd have the least distance.
|
||||
#
|
||||
# We need to keep doing this until we have visited all the nodes
|
||||
total = 0
|
||||
|
||||
while len(visited) < N:
|
||||
curr_dist, min_point = heappop(min_heap)
|
||||
|
||||
# It's possible we've already visited the node (let's say the very first node we
|
||||
# initialized the heap with) since it could end up being added to the heap again
|
||||
# while visiting other nodes. If this is the case, we skip this iteration of the
|
||||
# loop
|
||||
if min_point in visited:
|
||||
continue
|
||||
|
||||
total += curr_dist
|
||||
visited.add(min_point)
|
||||
|
||||
for neighbor in neighbors[min_point]:
|
||||
if neighbor[1] not in visited:
|
||||
heappush(min_heap, neighbor)
|
||||
|
||||
return total
|
||||
|
||||
|
||||
Loading…
Reference in New Issue
Block a user