balanced-binary-tree: add py3 soln
This commit is contained in:
parent
fdc24da4ff
commit
c53d6303b5
32
0110_balanced-binary-tree/README.md
Normal file
32
0110_balanced-binary-tree/README.md
Normal file
@ -0,0 +1,32 @@
|
|||||||
|
Given a binary tree, determine if it is height-balanced.
|
||||||
|
|
||||||
|
For this problem, a height-balanced binary tree is defined as:
|
||||||
|
|
||||||
|
> a binary tree in which the left and right subtrees of _every_ node differ in height by no more than 1.
|
||||||
|
|
||||||
|
**Example 1:**
|
||||||
|
|
||||||
|
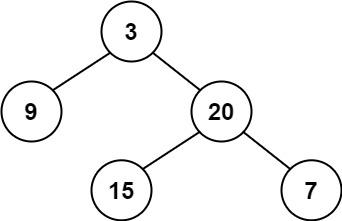
|
||||||
|
|
||||||
|
Input: root = [3,9,20,null,null,15,7]
|
||||||
|
Output: true
|
||||||
|
|
||||||
|
|
||||||
|
**Example 2:**
|
||||||
|
|
||||||
|
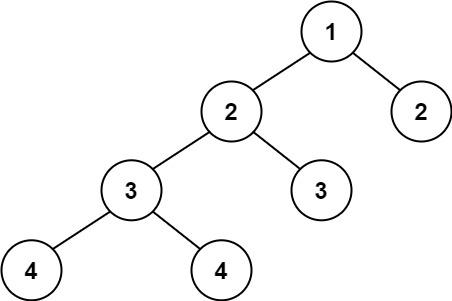
|
||||||
|
|
||||||
|
Input: root = [1,2,2,3,3,null,null,4,4]
|
||||||
|
Output: false
|
||||||
|
|
||||||
|
|
||||||
|
**Example 3:**
|
||||||
|
|
||||||
|
Input: root = []
|
||||||
|
Output: true
|
||||||
|
|
||||||
|
|
||||||
|
**Constraints:**
|
||||||
|
|
||||||
|
* The number of nodes in the tree is in the range `[0, 5000]`.
|
||||||
|
* `-104 <= Node.val <= 104`
|
||||||
47
0110_balanced-binary-tree/python3/solution.py
Normal file
47
0110_balanced-binary-tree/python3/solution.py
Normal file
@ -0,0 +1,47 @@
|
|||||||
|
# Time: O(N)
|
||||||
|
# Space: O(N)
|
||||||
|
|
||||||
|
# Definition for a binary tree node.
|
||||||
|
# class TreeNode:
|
||||||
|
# def __init__(self, val=0, left=None, right=None):
|
||||||
|
# self.val = val
|
||||||
|
# self.left = left
|
||||||
|
# self.right = right
|
||||||
|
from collections import namedtuple
|
||||||
|
|
||||||
|
class Solution:
|
||||||
|
def isBalanced(self, root: Optional[TreeNode]) -> bool:
|
||||||
|
Result = namedtuple('Result', 'is_balanced height')
|
||||||
|
|
||||||
|
def dfs(node):
|
||||||
|
"""
|
||||||
|
Instead of doing top-down, we'll do bottom-up recursion
|
||||||
|
via DFS to solve subproblems and bubble back up to the root
|
||||||
|
"""
|
||||||
|
|
||||||
|
# This happens when we reach leaf node, in which case, we assume
|
||||||
|
# things are balanced and return 0 height
|
||||||
|
if node is None: return Result(True, 0)
|
||||||
|
|
||||||
|
# DFS recursion
|
||||||
|
right = dfs(node.right)
|
||||||
|
left = dfs(node.left)
|
||||||
|
|
||||||
|
# For current `node`, things are only going to be balanced if
|
||||||
|
# both left and right subtrees are balanced. Otherwise, we can
|
||||||
|
# return False right away.
|
||||||
|
has_balanced_subtrees = right.is_balanced and left.is_balanced
|
||||||
|
|
||||||
|
# Besides having left and right subtrees themselves *individually*
|
||||||
|
# being balanced, we need to next check height difference <= 1.
|
||||||
|
if has_balanced_subtrees and abs(right.height - left.height) <= 1:
|
||||||
|
# Height of tree formed by current `node` would be the max
|
||||||
|
# height of its left/right subtree + 1 (itself)
|
||||||
|
return Result(True, 1 + max(left.height, right.height))
|
||||||
|
|
||||||
|
# If it reaches here, that means either height diff > 1 or left/right
|
||||||
|
# subtrees are already imbalanced.
|
||||||
|
return Result(False, 0)
|
||||||
|
|
||||||
|
|
||||||
|
return dfs(root).is_balanced
|
||||||
Loading…
Reference in New Issue
Block a user