path-with-minimum-effort py3
This commit is contained in:
parent
39191b4421
commit
f079950230
42
1753_path-with-minimum-effort/README.md
Normal file
42
1753_path-with-minimum-effort/README.md
Normal file
@ -0,0 +1,42 @@
|
|||||||
|
You are a hiker preparing for an upcoming hike. You are given `heights`, a 2D array of size `rows x columns`, where `heights[row][col]` represents the height of cell `(row, col)`. You are situated in the top-left cell, `(0, 0)`, and you hope to travel to the bottom-right cell, `(rows-1, columns-1)` (i.e., **0-indexed**). You can move **up**, **down**, **left**, or **right**, and you wish to find a route that requires the minimum **effort**.
|
||||||
|
|
||||||
|
A route's **effort** is the **maximum absolute difference** in heights between two consecutive cells of the route.
|
||||||
|
|
||||||
|
Return _the minimum **effort** required to travel from the top-left cell to the bottom-right cell._
|
||||||
|
|
||||||
|
**Example 1:**
|
||||||
|
|
||||||
|
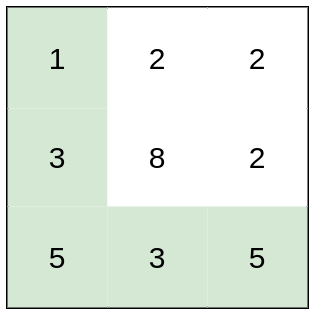
|
||||||
|
|
||||||
|
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
|
||||||
|
Output: 2
|
||||||
|
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
|
||||||
|
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
|
||||||
|
|
||||||
|
|
||||||
|
**Example 2:**
|
||||||
|
|
||||||
|
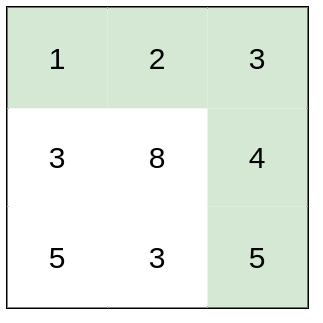
|
||||||
|
|
||||||
|
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
|
||||||
|
Output: 1
|
||||||
|
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
|
||||||
|
|
||||||
|
|
||||||
|
**Example 3:**
|
||||||
|
|
||||||
|
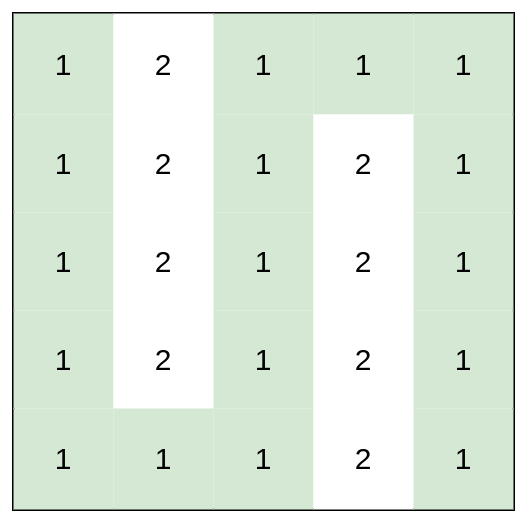
|
||||||
|
|
||||||
|
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
|
||||||
|
Output: 0
|
||||||
|
Explanation: This route does not require any effort.
|
||||||
|
|
||||||
|
|
||||||
|
**Constraints:**
|
||||||
|
|
||||||
|
* `rows == heights.length`
|
||||||
|
* `columns == heights[i].length`
|
||||||
|
* `1 <= rows, columns <= 100`
|
||||||
|
* `1 <= heights[i][j] <= 106`
|
||||||
|
|
||||||
|
https://leetcode.com/problems/path-with-minimum-effort/
|
||||||
65
1753_path-with-minimum-effort/python3/bfs_binary_search.py
Normal file
65
1753_path-with-minimum-effort/python3/bfs_binary_search.py
Normal file
@ -0,0 +1,65 @@
|
|||||||
|
# Time: O(M · N)
|
||||||
|
# Space: O(M · N)
|
||||||
|
from collections import deque
|
||||||
|
|
||||||
|
class Solution:
|
||||||
|
def minimumEffortPath(self, heights: List[List[int]]) -> int:
|
||||||
|
'''
|
||||||
|
BFS + Binary Search
|
||||||
|
|
||||||
|
Give attention to definition of minimum effort in the problem.
|
||||||
|
It's not the total across the path, but just between two
|
||||||
|
adjacent allowed cells.
|
||||||
|
'''
|
||||||
|
nrows, ncols = len(heights), len(heights[0])
|
||||||
|
|
||||||
|
def can_reach_destination(mid):
|
||||||
|
'''
|
||||||
|
Do BFS traversing min paths
|
||||||
|
'''
|
||||||
|
visited = set()
|
||||||
|
q = deque([(0, 0)])
|
||||||
|
destination = (nrows - 1, ncols - 1)
|
||||||
|
|
||||||
|
while q:
|
||||||
|
x, y = q.popleft()
|
||||||
|
|
||||||
|
# See if we reached the destination
|
||||||
|
if (x, y) == destination:
|
||||||
|
return True
|
||||||
|
|
||||||
|
visited.add((x, y))
|
||||||
|
|
||||||
|
dirs = [
|
||||||
|
(0, 1), # Right
|
||||||
|
(0, -1), # Left
|
||||||
|
(1, 0), # Bottom
|
||||||
|
(-1, 0) # Top
|
||||||
|
]
|
||||||
|
|
||||||
|
for dx, dy in dirs:
|
||||||
|
adj_x = x + dx
|
||||||
|
adj_y = y + dy
|
||||||
|
|
||||||
|
if 0 <= adj_x < nrows and 0 <= adj_y < ncols and (adj_x, adj_y) not in visited:
|
||||||
|
if abs(heights[x][y] - heights[adj_x][adj_y]) <= mid:
|
||||||
|
visited.add((adj_x, adj_y))
|
||||||
|
q.append((adj_x, adj_y))
|
||||||
|
|
||||||
|
return False
|
||||||
|
|
||||||
|
left = 0
|
||||||
|
right = 1e6 # As provided in the problem statement
|
||||||
|
|
||||||
|
# Perform binary search
|
||||||
|
while left < right:
|
||||||
|
mid = (left + right) // 2
|
||||||
|
|
||||||
|
# The answer could either be mid or an effort value
|
||||||
|
# lower than mid
|
||||||
|
if can_reach_destination(mid):
|
||||||
|
right = mid
|
||||||
|
else:
|
||||||
|
left = mid + 1
|
||||||
|
|
||||||
|
return int(left)
|
||||||
0
1753_path-with-minimum-effort/python3/solution.py
Normal file
0
1753_path-with-minimum-effort/python3/solution.py
Normal file
Loading…
Reference in New Issue
Block a user