count-good-nodes in bt: add py3 soln

0110_balanced-binary-tree/README.md

@@ -0,0 +1,32 @@
+Given a binary tree, determine if it is height-balanced.
+
+For this problem, a height-balanced binary tree is defined as:
+
+> a binary tree in which the left and right subtrees of _every_ node differ in height by no more than 1.
+
+**Example 1:**
+
+![](https://assets.leetcode.com/uploads/2020/10/06/balance_1.jpg)
+
+    Input: root = [3,9,20,null,null,15,7]
+    Output: true
+    
+
+**Example 2:**
+
+![](https://assets.leetcode.com/uploads/2020/10/06/balance_2.jpg)
+
+    Input: root = [1,2,2,3,3,null,null,4,4]
+    Output: false
+    
+
+**Example 3:**
+
+    Input: root = []
+    Output: true
+    
+
+**Constraints:**
+
+*   The number of nodes in the tree is in the range `[0, 5000]`.
+*   `-104 <= Node.val <= 104`

0110_balanced-binary-tree/python3/solution.py

@@ -0,0 +1,47 @@
+# Time: O(N)
+# Space: O(N)
+
+# Definition for a binary tree node.
+# class TreeNode:
+#     def __init__(self, val=0, left=None, right=None):
+#         self.val = val
+#         self.left = left
+#         self.right = right
+from collections import namedtuple
+
+class Solution:
+    def isBalanced(self, root: Optional[TreeNode]) -> bool:
+        Result = namedtuple('Result', 'is_balanced height')
+        
+        def dfs(node):
+            """
+            Instead of doing top-down, we'll do bottom-up recursion
+            via DFS to solve subproblems and bubble back up to the root
+            """
+            
+            # This happens when we reach leaf node, in which case, we assume
+            # things are balanced and return 0 height
+            if node is None: return Result(True, 0)
+            
+            # DFS recursion
+            right = dfs(node.right)
+            left = dfs(node.left)
+            
+            # For current `node`, things are only going to be balanced if
+            # both left and right subtrees are balanced. Otherwise, we can
+            # return False right away.
+            has_balanced_subtrees = right.is_balanced and left.is_balanced
+            
+            # Besides having left and right subtrees themselves *individually*
+            # being balanced, we need to next check height difference <= 1.
+            if has_balanced_subtrees and abs(right.height - left.height) <= 1:
+                # Height of tree formed by current `node` would be the max
+                # height of its left/right subtree + 1 (itself)
+                return Result(True, 1 + max(left.height, right.height))
+            
+            # If it reaches here, that means either height diff > 1 or left/right
+            # subtrees are already imbalanced.
+            return Result(False, 0)
+        
+        
+        return dfs(root).is_balanced

1544_count-good-nodes-in-binary-tree/README.md

@@ -0,0 +1,34 @@
+Given a binary tree `root`, a node _X_ in the tree is named **good** if in the path from root to _X_ there are no nodes with a value _greater than_ X.
+
+Return the number of **good** nodes in the binary tree.
+
+**Example 1:**
+
+**![](https://assets.leetcode.com/uploads/2020/04/02/test_sample_1.png)**
+
+    Input: root = [3,1,4,3,null,1,5]
+    Output: 4
+    Explanation: Nodes in blue are good.
+    Root Node (3) is always a good node.
+    Node 4 -> (3,4) is the maximum value in the path starting from the root.
+    Node 5 -> (3,4,5) is the maximum value in the path
+    Node 3 -> (3,1,3) is the maximum value in the path.
+
+**Example 2:**
+
+**![](https://assets.leetcode.com/uploads/2020/04/02/test_sample_2.png)**
+
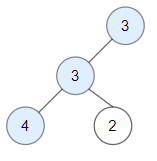
+    Input: root = [3,3,null,4,2]
+    Output: 3
+    Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.
+
+**Example 3:**
+
+    Input: root = [1]
+    Output: 1
+    Explanation: Root is considered as good.
+
+**Constraints:**
+
+*   The number of nodes in the binary tree is in the range `[1, 10^5]`.
+*   Each node's value is between `[-10^4, 10^4]`.

1544_count-good-nodes-in-binary-tree/python3/solution.py

@@ -0,0 +1,37 @@
+# Time: O(N)
+# Space: O(N)
+
+# Definition for a binary tree node.
+# class TreeNode:
+#     def __init__(self, val=0, left=None, right=None):
+#         self.val = val
+#         self.left = left
+#         self.right = right
+class Solution:
+    def goodNodes(self, root: TreeNode) -> int:
+        def dfs(node, max_value) -> int:
+            '''
+            Perform pre-order traversal and keep track of max
+            elements in the tree. Any subsequent traversal can
+            then compare against the updated max_value to see if
+            it's a good node or not
+            '''
+            
+            # If no left/right nodes, then we can just return 0
+            if not node: return 0
+            
+            # Current node is good if it's value is greater than or
+            # equal to the `max_value` seen so far
+            res = 1 if max_value <= node.val else 0
+            
+            # Compute the new max value, the current node could be it
+            max_value = max(max_value, node.val)
+            
+            # Do traversal on left and right nodes and add their units
+            res += dfs(node.left, max_value) + dfs(node.right, max_value)
+            
+            # This will indicate the count
+            return res
+        
+        
+        return dfs(root, root.val)