x/leetcode
1
0
Fork 0
Code Issues Pull Requests Projects Releases Wiki Activity

Compare commits

base: x:382be1e6839f2e935b6d095c2f24714f9405b315
Branches Tags
x:main
..
compare: x:58a19f7015d99704d72db0ff1ae82e6c07d058a9
Branches Tags
x:main

No commits in common. "382be1e6839f2e935b6d095c2f24714f9405b315" and "58a19f7015d99704d72db0ff1ae82e6c07d058a9" have entirely different histories.
382be1e683 ... 58a19f7015

8 changed files with 0 additions and 264 deletions
Show Stats Expand all files Collapse all files

29
0074_search-a-2d-matrix/README.md
View File

@ -1,29 +0,0 @@
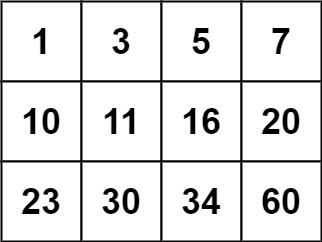
Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
* Integers in each row are sorted from left to right.
* The first integer of each row is greater than the last integer of the previous row.
**Example 1:**
![](https://assets.leetcode.com/uploads/2020/10/05/mat.jpg)
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true
**Example 2:**
![](https://assets.leetcode.com/uploads/2020/10/05/mat2.jpg)
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false
**Constraints:**
* `m == matrix.length`
* `n == matrix[i].length`
* `1 <= m, n <= 100`
* `-104 <= matrix[i][j], target <= 104`
https://leetcode.com/problems/search-a-2d-matrix/

42
0074_search-a-2d-matrix/python3/solution.py
View File

@ -1,42 +0,0 @@
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
'''
Two binary searches, first across rows and then
across columns to quickly find the target
'''
mid = -1
start, end = 0, len(matrix) - 1
# Figure out which row the number belongs to
while start <= end:
mid = (start + end) // 2
if target > matrix[mid][-1]:
start = mid + 1
elif target < matrix[mid][0]:
end = mid - 1
else:
break
# If we never managed to find a row, that means number
# doesn't exist
if not start <= end:
return False
# The row to search
row = matrix[mid]
start, end = 0, len(row) - 1
while start <= end:
mid = (start + end) // 2
if target == row[mid]:
return True
elif target > row[mid]:
start = mid + 1
else:
end = mid - 1
return False

28
0102_binary-tree-level-order-traversal/README.md
View File

@ -1,28 +0,0 @@
Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
**Example 1:**
![](https://assets.leetcode.com/uploads/2021/02/19/tree1.jpg)
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]
**Example 2:**
Input: root = [1]
Output: [[1]]
**Example 3:**
Input: root = []
Output: []
**Constraints:**
* The number of nodes in the tree is in the range `[0, 2000]`.
* `-1000 <= Node.val <= 1000`
https://leetcode.com/problems/binary-tree-level-order-traversal/

49
0102_binary-tree-level-order-traversal/python3/solution.py
View File

@ -1,49 +0,0 @@
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from collections import deque
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
'''
BFS
'''
if root is None: return []
q = deque([root])
results = []
while q:
n = len(q)
level = []
# Idea here is we iterate through the queue, the queue
# will always contain 1, 2, 4, 8 ... elements for each
# level since we'll be appending None .left/.right nodes
# also. This makes it easier to do the computation.
for i in range(n):
curr = q.popleft()
# Could be None, ignore if that's the case
if curr:
level.append(curr.val)
# It's okay to append None values here, the condition
# above will filter it out
q.append(curr.left)
q.append(curr.right)
# Since there's a chance that at the last level of the tree, we
# might be pushing None nodes due to .left/.right being None, we
# might have an empty level. We check and avoid adding the empty
# level in this case.
if level:
results.append(level)
return results

37
0235_lowest-common-ancestor-of-a-binary-search-tree/README.md
View File

@ -1,37 +0,0 @@
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): “The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**).”
**Example 1:**
![](https://assets.leetcode.com/uploads/2018/12/14/binarysearchtree_improved.png)
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
**Example 2:**
![](https://assets.leetcode.com/uploads/2018/12/14/binarysearchtree_improved.png)
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
**Example 3:**
Input: root = [2,1], p = 2, q = 1
Output: 2
**Constraints:**
* The number of nodes in the tree is in the range `[2, 105]`.
* `-109 <= Node.val <= 109`
* All `Node.val` are **unique**.
* `p != q`
* `p` and `q` will exist in the BST.
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree

25
0235_lowest-common-ancestor-of-a-binary-search-tree/python3/solution.py
View File

@ -1,25 +0,0 @@
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
curr = root
while curr:
# Both p and q can be found in right subtree so move
# curr there
if p.val > curr.val and q.val > curr.val:
curr = curr.right
# Both p and q can be found in left subtree so move
# curr there
elif p.val < curr.val and q.val < curr.val:
curr = curr.left
# If above cases fail, that means we are already at a `curr`
# where p exists in one side and q exists on another side so
# that must mean `curr` is the LCA
else:
return curr

28
0572_subtree-of-another-tree/README.md
View File

@ -1,28 +0,0 @@
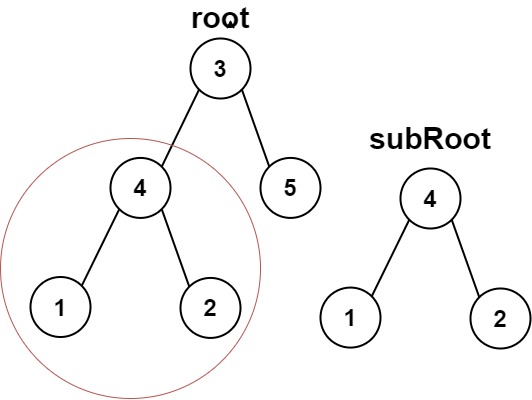
Given the roots of two binary trees `root` and `subRoot`, return `true` if there is a subtree of `root` with the same structure and node values of `subRoot` and `false` otherwise.
A subtree of a binary tree `tree` is a tree that consists of a node in `tree` and all of this node's descendants. The tree `tree` could also be considered as a subtree of itself.
**Example 1:**
![](https://assets.leetcode.com/uploads/2021/04/28/subtree1-tree.jpg)
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true
**Example 2:**
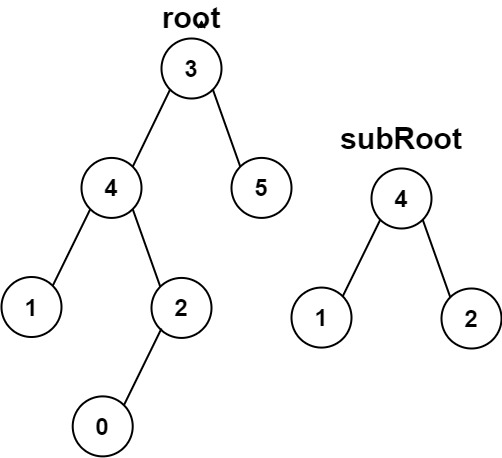
![](https://assets.leetcode.com/uploads/2021/04/28/subtree2-tree.jpg)
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false
**Constraints:**
* The number of nodes in the `root` tree is in the range `[1, 2000]`.
* The number of nodes in the `subRoot` tree is in the range `[1, 1000]`.
* `-104 <= root.val <= 104`
* `-104 <= subRoot.val <= 104`
https://leetcode.com/problems/subtree-of-another-tree

26
0572_subtree-of-another-tree/python3/solution.py
View File

@ -1,26 +0,0 @@
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if subRoot is None:
return True
elif root is None:
return False
if self.isSameTree(root, subRoot):
return True
return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)
def isSameTree(self, a, b):
if a is None and b is None:
return True
elif a is None or b is None or a.val != b.val:
return False
return self.isSameTree(a.left, b.left) and self.isSameTree(a.right, b.right)