Compare commits
4 Commits
58a19f7015
...
382be1e683
| Author | SHA1 | Date | |
|---|---|---|---|
| 382be1e683 | |||
| 6925c6815f | |||
| 91cc45db21 | |||
| acc9f4eaea |
29
0074_search-a-2d-matrix/README.md
Normal file
29
0074_search-a-2d-matrix/README.md
Normal file
@ -0,0 +1,29 @@
|
|||||||
|
Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
|
||||||
|
|
||||||
|
* Integers in each row are sorted from left to right.
|
||||||
|
* The first integer of each row is greater than the last integer of the previous row.
|
||||||
|
|
||||||
|
**Example 1:**
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
|
||||||
|
Output: true
|
||||||
|
|
||||||
|
|
||||||
|
**Example 2:**
|
||||||
|
|
||||||
|
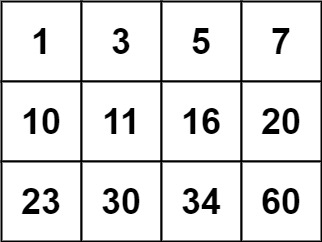
|
||||||
|
|
||||||
|
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
|
||||||
|
Output: false
|
||||||
|
|
||||||
|
|
||||||
|
**Constraints:**
|
||||||
|
|
||||||
|
* `m == matrix.length`
|
||||||
|
* `n == matrix[i].length`
|
||||||
|
* `1 <= m, n <= 100`
|
||||||
|
* `-104 <= matrix[i][j], target <= 104`
|
||||||
|
|
||||||
|
https://leetcode.com/problems/search-a-2d-matrix/
|
||||||
42
0074_search-a-2d-matrix/python3/solution.py
Normal file
42
0074_search-a-2d-matrix/python3/solution.py
Normal file
@ -0,0 +1,42 @@
|
|||||||
|
class Solution:
|
||||||
|
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
|
||||||
|
'''
|
||||||
|
Two binary searches, first across rows and then
|
||||||
|
across columns to quickly find the target
|
||||||
|
'''
|
||||||
|
|
||||||
|
mid = -1
|
||||||
|
start, end = 0, len(matrix) - 1
|
||||||
|
|
||||||
|
# Figure out which row the number belongs to
|
||||||
|
while start <= end:
|
||||||
|
mid = (start + end) // 2
|
||||||
|
|
||||||
|
if target > matrix[mid][-1]:
|
||||||
|
start = mid + 1
|
||||||
|
elif target < matrix[mid][0]:
|
||||||
|
end = mid - 1
|
||||||
|
else:
|
||||||
|
break
|
||||||
|
|
||||||
|
# If we never managed to find a row, that means number
|
||||||
|
# doesn't exist
|
||||||
|
if not start <= end:
|
||||||
|
return False
|
||||||
|
|
||||||
|
# The row to search
|
||||||
|
row = matrix[mid]
|
||||||
|
start, end = 0, len(row) - 1
|
||||||
|
|
||||||
|
while start <= end:
|
||||||
|
mid = (start + end) // 2
|
||||||
|
|
||||||
|
if target == row[mid]:
|
||||||
|
return True
|
||||||
|
elif target > row[mid]:
|
||||||
|
start = mid + 1
|
||||||
|
else:
|
||||||
|
end = mid - 1
|
||||||
|
|
||||||
|
return False
|
||||||
|
|
||||||
28
0102_binary-tree-level-order-traversal/README.md
Normal file
28
0102_binary-tree-level-order-traversal/README.md
Normal file
@ -0,0 +1,28 @@
|
|||||||
|
Given the `root` of a binary tree, return _the level order traversal of its nodes' values_. (i.e., from left to right, level by level).
|
||||||
|
|
||||||
|
**Example 1:**
|
||||||
|
|
||||||
|
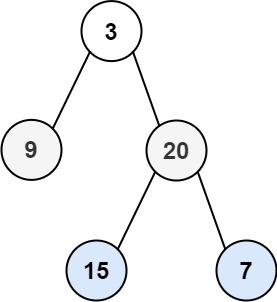
|
||||||
|
|
||||||
|
Input: root = [3,9,20,null,null,15,7]
|
||||||
|
Output: [[3],[9,20],[15,7]]
|
||||||
|
|
||||||
|
|
||||||
|
**Example 2:**
|
||||||
|
|
||||||
|
Input: root = [1]
|
||||||
|
Output: [[1]]
|
||||||
|
|
||||||
|
|
||||||
|
**Example 3:**
|
||||||
|
|
||||||
|
Input: root = []
|
||||||
|
Output: []
|
||||||
|
|
||||||
|
|
||||||
|
**Constraints:**
|
||||||
|
|
||||||
|
* The number of nodes in the tree is in the range `[0, 2000]`.
|
||||||
|
* `-1000 <= Node.val <= 1000`
|
||||||
|
|
||||||
|
https://leetcode.com/problems/binary-tree-level-order-traversal/
|
||||||
49
0102_binary-tree-level-order-traversal/python3/solution.py
Normal file
49
0102_binary-tree-level-order-traversal/python3/solution.py
Normal file
@ -0,0 +1,49 @@
|
|||||||
|
# Definition for a binary tree node.
|
||||||
|
# class TreeNode:
|
||||||
|
# def __init__(self, val=0, left=None, right=None):
|
||||||
|
# self.val = val
|
||||||
|
# self.left = left
|
||||||
|
# self.right = right
|
||||||
|
|
||||||
|
from collections import deque
|
||||||
|
|
||||||
|
class Solution:
|
||||||
|
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
|
||||||
|
'''
|
||||||
|
BFS
|
||||||
|
'''
|
||||||
|
|
||||||
|
if root is None: return []
|
||||||
|
|
||||||
|
q = deque([root])
|
||||||
|
results = []
|
||||||
|
|
||||||
|
while q:
|
||||||
|
n = len(q)
|
||||||
|
|
||||||
|
level = []
|
||||||
|
# Idea here is we iterate through the queue, the queue
|
||||||
|
# will always contain 1, 2, 4, 8 ... elements for each
|
||||||
|
# level since we'll be appending None .left/.right nodes
|
||||||
|
# also. This makes it easier to do the computation.
|
||||||
|
for i in range(n):
|
||||||
|
curr = q.popleft()
|
||||||
|
|
||||||
|
# Could be None, ignore if that's the case
|
||||||
|
if curr:
|
||||||
|
level.append(curr.val)
|
||||||
|
|
||||||
|
# It's okay to append None values here, the condition
|
||||||
|
# above will filter it out
|
||||||
|
q.append(curr.left)
|
||||||
|
q.append(curr.right)
|
||||||
|
|
||||||
|
# Since there's a chance that at the last level of the tree, we
|
||||||
|
# might be pushing None nodes due to .left/.right being None, we
|
||||||
|
# might have an empty level. We check and avoid adding the empty
|
||||||
|
# level in this case.
|
||||||
|
if level:
|
||||||
|
results.append(level)
|
||||||
|
|
||||||
|
return results
|
||||||
|
|
||||||
@ -0,0 +1,37 @@
|
|||||||
|
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
|
||||||
|
|
||||||
|
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): “The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**).”
|
||||||
|
|
||||||
|
**Example 1:**
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
|
||||||
|
Output: 6
|
||||||
|
Explanation: The LCA of nodes 2 and 8 is 6.
|
||||||
|
|
||||||
|
|
||||||
|
**Example 2:**
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
|
||||||
|
Output: 2
|
||||||
|
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
|
||||||
|
|
||||||
|
|
||||||
|
**Example 3:**
|
||||||
|
|
||||||
|
Input: root = [2,1], p = 2, q = 1
|
||||||
|
Output: 2
|
||||||
|
|
||||||
|
|
||||||
|
**Constraints:**
|
||||||
|
|
||||||
|
* The number of nodes in the tree is in the range `[2, 105]`.
|
||||||
|
* `-109 <= Node.val <= 109`
|
||||||
|
* All `Node.val` are **unique**.
|
||||||
|
* `p != q`
|
||||||
|
* `p` and `q` will exist in the BST.
|
||||||
|
|
||||||
|
https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree
|
||||||
@ -0,0 +1,25 @@
|
|||||||
|
# Definition for a binary tree node.
|
||||||
|
# class TreeNode:
|
||||||
|
# def __init__(self, x):
|
||||||
|
# self.val = x
|
||||||
|
# self.left = None
|
||||||
|
# self.right = None
|
||||||
|
|
||||||
|
class Solution:
|
||||||
|
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
|
||||||
|
curr = root
|
||||||
|
|
||||||
|
while curr:
|
||||||
|
# Both p and q can be found in right subtree so move
|
||||||
|
# curr there
|
||||||
|
if p.val > curr.val and q.val > curr.val:
|
||||||
|
curr = curr.right
|
||||||
|
# Both p and q can be found in left subtree so move
|
||||||
|
# curr there
|
||||||
|
elif p.val < curr.val and q.val < curr.val:
|
||||||
|
curr = curr.left
|
||||||
|
# If above cases fail, that means we are already at a `curr`
|
||||||
|
# where p exists in one side and q exists on another side so
|
||||||
|
# that must mean `curr` is the LCA
|
||||||
|
else:
|
||||||
|
return curr
|
||||||
28
0572_subtree-of-another-tree/README.md
Normal file
28
0572_subtree-of-another-tree/README.md
Normal file
@ -0,0 +1,28 @@
|
|||||||
|
Given the roots of two binary trees `root` and `subRoot`, return `true` if there is a subtree of `root` with the same structure and node values of `subRoot` and `false` otherwise.
|
||||||
|
|
||||||
|
A subtree of a binary tree `tree` is a tree that consists of a node in `tree` and all of this node's descendants. The tree `tree` could also be considered as a subtree of itself.
|
||||||
|
|
||||||
|
**Example 1:**
|
||||||
|
|
||||||
|
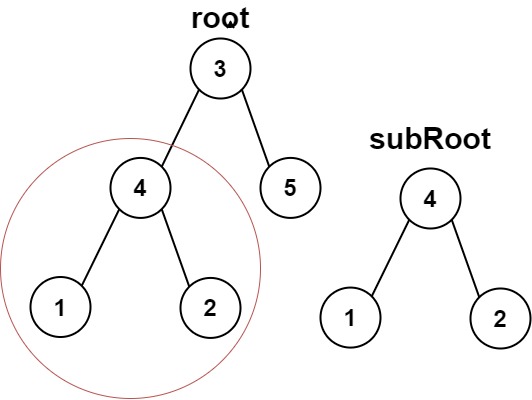
|
||||||
|
|
||||||
|
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
|
||||||
|
Output: true
|
||||||
|
|
||||||
|
|
||||||
|
**Example 2:**
|
||||||
|
|
||||||
|
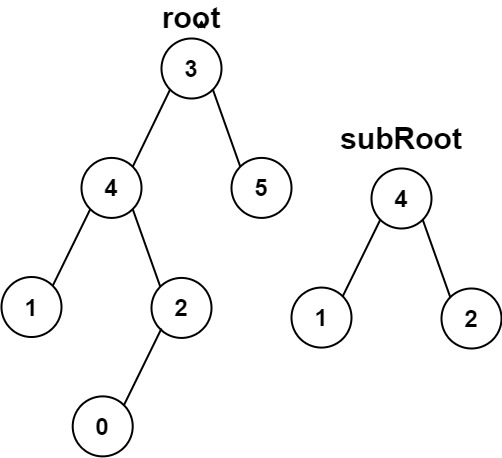
|
||||||
|
|
||||||
|
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
|
||||||
|
Output: false
|
||||||
|
|
||||||
|
|
||||||
|
**Constraints:**
|
||||||
|
|
||||||
|
* The number of nodes in the `root` tree is in the range `[1, 2000]`.
|
||||||
|
* The number of nodes in the `subRoot` tree is in the range `[1, 1000]`.
|
||||||
|
* `-104 <= root.val <= 104`
|
||||||
|
* `-104 <= subRoot.val <= 104`
|
||||||
|
|
||||||
|
https://leetcode.com/problems/subtree-of-another-tree
|
||||||
26
0572_subtree-of-another-tree/python3/solution.py
Normal file
26
0572_subtree-of-another-tree/python3/solution.py
Normal file
@ -0,0 +1,26 @@
|
|||||||
|
# Definition for a binary tree node.
|
||||||
|
# class TreeNode:
|
||||||
|
# def __init__(self, val=0, left=None, right=None):
|
||||||
|
# self.val = val
|
||||||
|
# self.left = left
|
||||||
|
# self.right = right
|
||||||
|
class Solution:
|
||||||
|
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
|
||||||
|
if subRoot is None:
|
||||||
|
return True
|
||||||
|
elif root is None:
|
||||||
|
return False
|
||||||
|
|
||||||
|
if self.isSameTree(root, subRoot):
|
||||||
|
return True
|
||||||
|
|
||||||
|
return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)
|
||||||
|
|
||||||
|
|
||||||
|
def isSameTree(self, a, b):
|
||||||
|
if a is None and b is None:
|
||||||
|
return True
|
||||||
|
elif a is None or b is None or a.val != b.val:
|
||||||
|
return False
|
||||||
|
|
||||||
|
return self.isSameTree(a.left, b.left) and self.isSameTree(a.right, b.right)
|
||||||
Loading…
Reference in New Issue
Block a user