Compare commits
3 Commits
e793d395bd
...
58a19f7015
| Author | SHA1 | Date | |
|---|---|---|---|
| 58a19f7015 | |||
| cccdd9269f | |||
| 713154644b |
34
0100_same-tree/README.md
Normal file
34
0100_same-tree/README.md
Normal file
@ -0,0 +1,34 @@
|
||||
Given the roots of two binary trees `p` and `q`, write a function to check if they are the same or not.
|
||||
|
||||
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
|
||||
|
||||
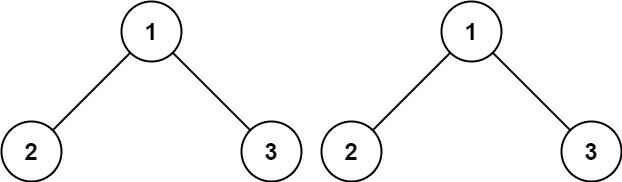
**Example 1:**
|
||||
|
||||
|
||||
|
||||
Input: p = [1,2,3], q = [1,2,3]
|
||||
Output: true
|
||||
|
||||
|
||||
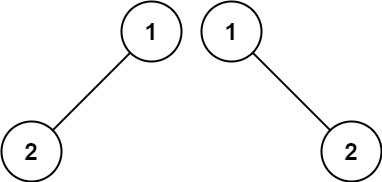
**Example 2:**
|
||||
|
||||
|
||||
|
||||
Input: p = [1,2], q = [1,null,2]
|
||||
Output: false
|
||||
|
||||
|
||||
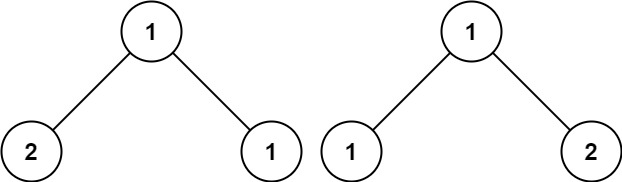
**Example 3:**
|
||||
|
||||
|
||||
|
||||
Input: p = [1,2,1], q = [1,1,2]
|
||||
Output: false
|
||||
|
||||
|
||||
**Constraints:**
|
||||
|
||||
* The number of nodes in both trees is in the range `[0, 100]`.
|
||||
* `-104 <= Node.val <= 104`
|
||||
|
||||
https://leetcode.com/problems/same-tree/
|
||||
14
0100_same-tree/python3/solution.py
Normal file
14
0100_same-tree/python3/solution.py
Normal file
@ -0,0 +1,14 @@
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
|
||||
if p is None and q is None:
|
||||
return True
|
||||
elif p is None or q is None or p.val != q.val:
|
||||
return False
|
||||
|
||||
return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
|
||||
24
0104_maximum-depth-of-binary-tree/README.md
Normal file
24
0104_maximum-depth-of-binary-tree/README.md
Normal file
@ -0,0 +1,24 @@
|
||||
Given the `root` of a binary tree, return _its maximum depth_.
|
||||
|
||||
A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
|
||||
|
||||
**Example 1:**
|
||||
|
||||

|
||||
|
||||
Input: root = [3,9,20,null,null,15,7]
|
||||
Output: 3
|
||||
|
||||
|
||||
**Example 2:**
|
||||
|
||||
Input: root = [1,null,2]
|
||||
Output: 2
|
||||
|
||||
|
||||
**Constraints:**
|
||||
|
||||
* The number of nodes in the tree is in the range `[0, 104]`.
|
||||
* `-100 <= Node.val <= 100`
|
||||
|
||||
https://leetcode.com/problems/maximum-depth-of-binary-tree
|
||||
0
0104_maximum-depth-of-binary-tree/python3/bfs.py
Normal file
0
0104_maximum-depth-of-binary-tree/python3/bfs.py
Normal file
@ -0,0 +1,27 @@
|
||||
# Time: O(N)
|
||||
# Space: O(N)
|
||||
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
maxDepthValue = 0
|
||||
|
||||
def maxDepth(self, root: Optional[TreeNode]) -> int:
|
||||
'''
|
||||
Recursive DFS pre-order but storing max globally
|
||||
'''
|
||||
def findMax(node, depth):
|
||||
if node is None: return None
|
||||
|
||||
currDepth = depth + 1
|
||||
self.maxDepthValue = max(currDepth, self.maxDepthValue)
|
||||
findMax(node.left, currDepth)
|
||||
findMax(node.right, currDepth)
|
||||
|
||||
findMax(root, 0)
|
||||
|
||||
return self.maxDepthValue
|
||||
@ -0,0 +1,17 @@
|
||||
# Time: O(N)
|
||||
# Space: O(N)
|
||||
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
maxDepthValue = 0
|
||||
|
||||
def maxDepth(self, root: Optional[TreeNode]) -> int:
|
||||
'''
|
||||
Recursive DFS
|
||||
'''
|
||||
return 0 if root is None else 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
|
||||
27
0543_diameter-of-binary-tree/README.md
Normal file
27
0543_diameter-of-binary-tree/README.md
Normal file
@ -0,0 +1,27 @@
|
||||
Given the `root` of a binary tree, return _the length of the **diameter** of the tree_.
|
||||
|
||||
The **diameter** of a binary tree is the **length** of the longest path between any two nodes in a tree. This path may or may not pass through the `root`.
|
||||
|
||||
The **length** of a path between two nodes is represented by the number of edges between them.
|
||||
|
||||
**Example 1:**
|
||||
|
||||

|
||||
|
||||
Input: root = [1,2,3,4,5]
|
||||
Output: 3
|
||||
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
|
||||
|
||||
|
||||
**Example 2:**
|
||||
|
||||
Input: root = [1,2]
|
||||
Output: 1
|
||||
|
||||
|
||||
**Constraints:**
|
||||
|
||||
* The number of nodes in the tree is in the range `[1, 104]`.
|
||||
* `-100 <= Node.val <= 100`
|
||||
|
||||
https://leetcode.com/problems/diameter-of-binary-tree/
|
||||
36
0543_diameter-of-binary-tree/python3/solution.py
Normal file
36
0543_diameter-of-binary-tree/python3/solution.py
Normal file
@ -0,0 +1,36 @@
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
|
||||
result = [0]
|
||||
|
||||
def dfs(node):
|
||||
# Leaf node height will be 1
|
||||
# Empty node height will be -1
|
||||
|
||||
if node is None: return -1
|
||||
|
||||
lefth = dfs(node.left)
|
||||
righth = dfs(node.right)
|
||||
|
||||
# Diameter calc:
|
||||
#
|
||||
# Cause for current node will be pointing to both
|
||||
# left and right nodes and we need to consider
|
||||
# them (+2)
|
||||
#
|
||||
# e.g. consider this is leaf node, lefth and righth = -1
|
||||
# so, current node's diameter should be 0 = 2 + -1 + -1
|
||||
result[0] = max(result[0], 2 + lefth + righth)
|
||||
|
||||
# return max height including the node itself
|
||||
return 1 + max(lefth, righth)
|
||||
|
||||
dfs(root)
|
||||
|
||||
return result[0]
|
||||
|
||||
Loading…
Reference in New Issue
Block a user