same-tree py3

0100_same-tree/README.md

@@ -0,0 +1,34 @@
+Given the roots of two binary trees `p` and `q`, write a function to check if they are the same or not.
+
+Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
+
+**Example 1:**
+
+![](https://assets.leetcode.com/uploads/2020/12/20/ex1.jpg)
+
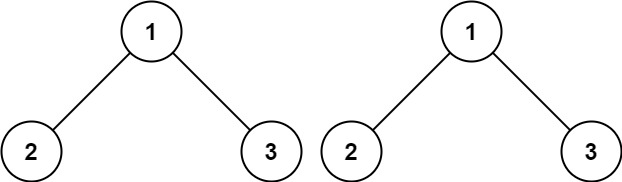
+    Input: p = [1,2,3], q = [1,2,3]
+    Output: true
+    
+
+**Example 2:**
+
+![](https://assets.leetcode.com/uploads/2020/12/20/ex2.jpg)
+
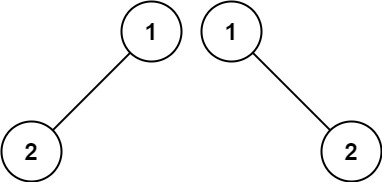
+    Input: p = [1,2], q = [1,null,2]
+    Output: false
+    
+
+**Example 3:**
+
+![](https://assets.leetcode.com/uploads/2020/12/20/ex3.jpg)
+
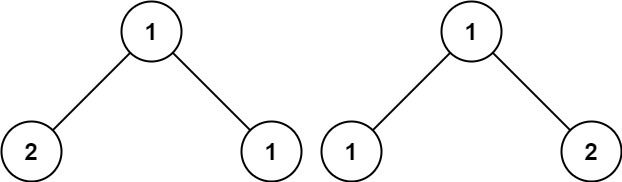
+    Input: p = [1,2,1], q = [1,1,2]
+    Output: false
+    
+
+**Constraints:**
+
+*   The number of nodes in both trees is in the range `[0, 100]`.
+*   `-104 <= Node.val <= 104`
+
+https://leetcode.com/problems/same-tree/

0100_same-tree/python3/solution.py

@@ -0,0 +1,14 @@
+# Definition for a binary tree node.
+# class TreeNode:
+#     def __init__(self, val=0, left=None, right=None):
+#         self.val = val
+#         self.left = left
+#         self.right = right
+class Solution:
+    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
+        if p is None and q is None:
+            return True
+        elif p is None or q is None or p.val != q.val:
+            return False
+        
+        return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

0104_maximum-depth-of-binary-tree/README.md

@@ -0,0 +1,24 @@
+Given the `root` of a binary tree, return _its maximum depth_.
+
+A binary tree's **maximum depth** is the number of nodes along the longest path from the root node down to the farthest leaf node.
+
+**Example 1:**
+
+![](https://assets.leetcode.com/uploads/2020/11/26/tmp-tree.jpg)
+
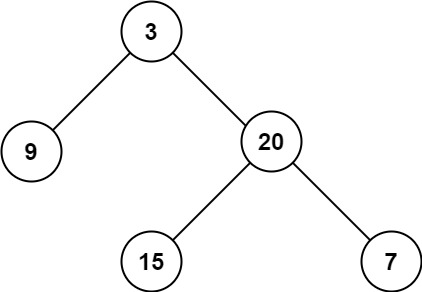
+    Input: root = [3,9,20,null,null,15,7]
+    Output: 3
+    
+
+**Example 2:**
+
+    Input: root = [1,null,2]
+    Output: 2
+    
+
+**Constraints:**
+
+*   The number of nodes in the tree is in the range `[0, 104]`.
+*   `-100 <= Node.val <= 100`
+
+https://leetcode.com/problems/maximum-depth-of-binary-tree

0104_maximum-depth-of-binary-tree/python3/dfs-pre-order-global.py

@@ -0,0 +1,27 @@
+# Time: O(N)
+# Space: O(N)
+
+# Definition for a binary tree node.
+# class TreeNode:
+#     def __init__(self, val=0, left=None, right=None):
+#         self.val = val
+#         self.left = left
+#         self.right = right
+class Solution:
+    maxDepthValue = 0
+    
+    def maxDepth(self, root: Optional[TreeNode]) -> int:
+        '''
+        Recursive DFS pre-order but storing max globally
+        '''
+        def findMax(node, depth):
+            if node is None: return None
+            
+            currDepth = depth + 1
+            self.maxDepthValue = max(currDepth, self.maxDepthValue)
+            findMax(node.left, currDepth)
+            findMax(node.right, currDepth)
+        
+        findMax(root, 0)
+        
+        return self.maxDepthValue

0104_maximum-depth-of-binary-tree/python3/dfs-pre-order-oneliner.py

@@ -0,0 +1,17 @@
+# Time: O(N)
+# Space: O(N)
+
+# Definition for a binary tree node.
+# class TreeNode:
+#     def __init__(self, val=0, left=None, right=None):
+#         self.val = val
+#         self.left = left
+#         self.right = right
+class Solution:
+    maxDepthValue = 0
+    
+    def maxDepth(self, root: Optional[TreeNode]) -> int:
+        '''
+        Recursive DFS
+        '''
+        return 0 if root is None else 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

0543_diameter-of-binary-tree/README.md

@@ -0,0 +1,27 @@
+Given the `root` of a binary tree, return _the length of the **diameter** of the tree_.
+
+The **diameter** of a binary tree is the **length** of the longest path between any two nodes in a tree. This path may or may not pass through the `root`.
+
+The **length** of a path between two nodes is represented by the number of edges between them.
+
+**Example 1:**
+
+![](https://assets.leetcode.com/uploads/2021/03/06/diamtree.jpg)
+
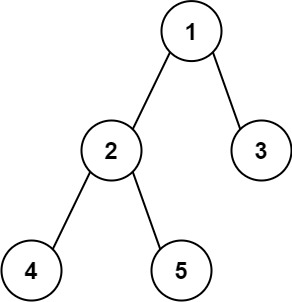
+    Input: root = [1,2,3,4,5]
+    Output: 3
+    Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
+    
+
+**Example 2:**
+
+    Input: root = [1,2]
+    Output: 1
+    
+
+**Constraints:**
+
+*   The number of nodes in the tree is in the range `[1, 104]`.
+*   `-100 <= Node.val <= 100`
+
+https://leetcode.com/problems/diameter-of-binary-tree/

0543_diameter-of-binary-tree/python3/solution.py

@@ -0,0 +1,36 @@
+# Definition for a binary tree node.
+# class TreeNode:
+#     def __init__(self, val=0, left=None, right=None):
+#         self.val = val
+#         self.left = left
+#         self.right = right
+class Solution:
+    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
+        result = [0]
+        
+        def dfs(node):
+            # Leaf node height will be 1
+            # Empty node height will be -1
+            
+            if node is None: return -1
+            
+            lefth = dfs(node.left)
+            righth = dfs(node.right)
+            
+            # Diameter calc:
+            #
+            # Cause for current node will be pointing to both
+            # left and right nodes and we need to consider
+            # them (+2)
+            #
+            # e.g. consider this is leaf node, lefth and righth = -1
+            # so, current node's diameter should be 0 = 2 + -1 + -1
+            result[0] = max(result[0], 2 + lefth + righth)
+            
+            # return max height including the node itself
+            return 1 + max(lefth, righth)
+        
+        dfs(root)
+        
+        return result[0]
+